cover

Signal Processing for Communications

by Paolo Prandoni and Martin Vetterli

Errata

Chapter 1:

  • Page 1; (First page, first line and a typo: that's a good start!) Is a a formal description
  • Page 4; line 11: the the side
  • Page 10; Eq. (1.4): strictly speaking, the fraction is not defined for t = nT_s but here we implicity invoke the continuity extension used in the definition of the sinc (see 5.34)
  • Page 13; the noise function is of obviously unknown
  • Page 17; Line 7: the voice signal ends up buried
  • Page 18; Further Reading, 7th line: integrated supplemented

Chapter 2:

  • Page 20; Eq 2.1: $x[n] = ((n + 5) mod 11) - 5$
  • Page 24; Eq 2.1: $x[n] = An example of (2.9) (2.10) is shown in Figure 2.5(d)
  • Page 26; Section "Shift": "to the left" and "to the right" are inverted in the text. A delay is a shift to the right, while an advancement is a shift to the left.
  • Page 29; Sec 2.2.1, Line 1: length N are is
  • Page 29; Line 12: ans and
  • Page 29; Line 14: are is
  • Page 30; Line 2: always finite
  • Page 32; Line 5: the the
  • Page 36; Exercise 2.1, item (d): i = 0, 1, 23.

Chapter 3:

  • Page 41; End of Section 3.1: Another important orthonormal basis for \mathbb{R}^N\mathbb{C}^N is the normalized Fourier basis...
  • Page 44; Line 12 from bottom: norme
  • Page 44; Line 9 from bottom: Cauchy-Schwartz
  • Page 45; Line 10: separate separable
  • Page 48; Eq. (3.36) and (3.37): the equations should adhere to a better formalism and be rewritten as: for (3.36): x \isin P and y \isin P => x + y \isin P; for (3.37): x \isin P and \alpha \isin S => \alpha x \isin P.
  • Page 49; line 13 from the top: Alternatively, an linearly independent set of vectors...
  • Page 50; Line 10 from the top: subscript l goes from zero to L-1
  • Page 50; Eq. (3.46): \arg\min_{\hat{\mathbf{y}} \in P} \|\mathbf{y - \hat{y}}\|_2 = \mathbf{d}. \sum_{k=0}^{K-1} \langle \mathbf{x}^{(k)}, \mathbf{y} \rangle \mathbf{x}^{(k)}.
  • Page 54; Eq. (3.59): probably a better notation for the subscript of the sum would be l \in \mathcal{Z} / \{k\}.

Chapter 4:

  • Page 61; Line 8: (with $N \neq 0$ obviously).
  • Page 67; Line 16: oscillatory behavior at frequency $2\pi/k$, $(2\pi/N)k$ is contained in the signal;
  • Page 69; Line 2: hot that of the original signal's
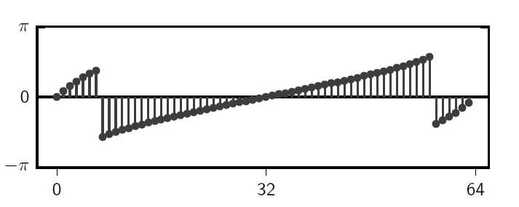
  • Page 70; Figure 4.8, bottom panel shows the phase for the DFT of $\cos((2\pi/5) n)$. The correct phase plot is the following:
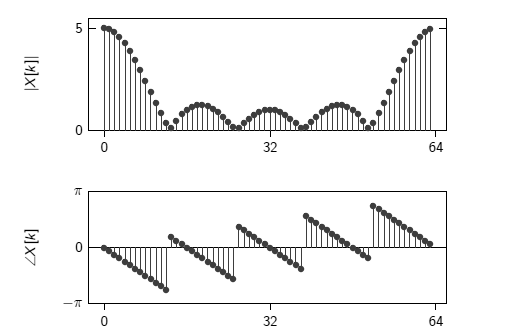
  • Page 71; Figure 4.9: the figure got slightly mangled in the typesetting process. A more accurate version is the following:
  • Page 73; 2nd formula: $/d\omega$ missing in the integral
  • Page 73; Eq. (4.16): spurious "=" sign after "lim"
  • Page 82; Line 6: Now we recognize in the last term important to recognize the last terms
  • Page 86; Eq 4.73: [ [x[N-k] x[N-k+1] \ldots x[N-1] x[0] x[1] x[2] \ldots x[N-k-1] ]^T
  • Page 89; Line 6 from the bottom: $x[n] = \delta[n-k]$ & $X[k] = e^{-j\frac{2\pi}{N}k}$ should be $x[n] = \delta[n-M]$ & $X[k] = e^{-j\frac{2\pi}{N}Mk}$
  • Page 92; Line 3 from bottom: precised made precise

Chapter 5:

  • Page 113; 2nd line of Section 5.2.2: $h[n] = \mathcal{H}\{x[n]\}$ $h[n] = \mathcal{H}\{\delta[n]\}$
  • Page 123; Line 4 from bottom: into three four broad categories
  • Page 125; Eq. (5.23): \angle{H(e^{j\omega})} = e^{-j\omega d} -\omega d
  • Page 130; Line 4: is only be in the mean square sense.
  • Page 132; Eq. 5.44: there should be no minus sign before the sine: $h[n] \ast \cos(\omega_0 n) = \sin(\omega_0 n)$
  • Page 135; Code example: indices are mangled: 
          // Shift delay line for x:
      for (k = M-1; k > 0; k--)
        x[k] = x[k-1];

      // new input value x[n]:
      x[0] = input;

      // Shift delay line for y:
      for (k = N-1; k > 0; k--)
        y[k] = y[k-1];

      double y = 0;
      for (k = 0; k < M; k++)
        y += b[k] * x[k];
      for (k = 1; k < N; k++)
        y -= a[k] * y[k];

Chapter 6:

  • Page 149; Eq (6.8): $X_1(z) = $.
  • Page 149; Eq (6.9): $X_2(z) = $.
  • Page 151; Line 18 (last equation): |x[n]z_0^n| <= |x[n]z_1^n| |x[n]z_1^n| <= |x[n]z_0^n|
  • Page 151; Fig 6.1 (label): (b) anticausal (b) sequence
  • Page 152; Line 8 from bottom: largest smallest magnitude
  • Page 156; last line: it is easy to see that the poles zeros of the filter are...
  • Page 157; Eq. (6.17): wrong exponent for z: (1-W_N^k z^{-k}) (1-W_N^k z^{-1})

Chapter 7:

  • Page 173; 2nd line from the top: by using only $2N+1$ Fourier coefficients terms in the Fourier sum
  • Page 173; Eq. (7.3): w[n] = \rect{n}{N} \rect{n}{2N}
  • Page 174; 2nd bullet point: $\Delta=4\pi(2N+1)$ $\Delta=4\pi/(2N+1)$
  • Page 174; line 4 (1st equation): in the convolution, the first factor should be H(e^(j\theta)) and not H(e^j\omega)
  • Page 175; line 3 (1st equation): the argument of the integral should be W(e^j(\omega_0 - \theta)) and not W(e^j(\omega - \omega_0))
  • Page 183; 3rd line from the bottom: polynomial degree $K$ $L
  • Page 187; line 18: except possibly in $x=0$ $x=-1$ or $x=1$
  • Page 187; line 20: the frequency response must be alternation alternating
  • Page 191; line 6 from bottom: at $\omega = 0$ times divided by the length of the signal's support
  • Page 192; line 14 from top cost/benefit tradeoff benefit-cost tradeoff
  • Page 196; 2nd line after eq. (7.27): $M_r + 2M_c = M$ $M_r + 2M_c = M-1$; a little later: $N_r + 2N_c = N$ $N_r + 2N_c = N-1$.
  • Page 198; Figures 7.24 to 7.27: all the $a$ coefficients in the filter structures should have a leading minus sign, as per eq. (5.47).
  • Page 213; Exercise 7.8, item (c): The zero of the transfer function is at z_0 = 1.8 + 0.4j, not at z_0 = -1.8 + 0.4j.

Chapter 8:

  • Page 221; line 4 from bottom: missing bracket: R_X[l, k] = E[X[l]X[k]]
  • Page 226; Eq. (8.16): P_XY(e^(j\omega)) P_{XY}(e^(j\omega)) = \sum_{t = -\infty} {k = -\infty} ...
  • Page 228; Eq. (8.19), first line: E[\sum_{k = 0} {k = -\infty} ...

Chapter 9:

  • Page 238; Eq 9.6 $\FT{e^{j\Omega_0 t}} = 2\pi\delta(\Omega-\Omega_0)$
  • Page 239; Equation (9.9): Eq. (9.9) the denominator of the first term in the right-hand side should be \Omega_N and not \Omega_s.
  • Page 248; Equation (9.9): Second unnumbered equation after Eq. (9.9), first line, right-hand side: it should be \rect(\frac{\Omega}{2Omega_N}) (i.e. the denominator in the argument to the rect misses a leading "2").
  • Page 249; Equation (9.22): it should be \rect(\frac{\Omega}{2Omega_N}) (i.e. the denominator in the argument to the rect misses a leading "2").
  • Page 252; Lines 9, 10 and 13: replace $(1+\alpha)$ by $(2-\alpha$): "If we increase the frequency further, say to $f_0 = (2-\alpha)F_N$, we have \[ x[n] = e^{j(2-\alpha)\pi n = e^{-j\alpha \pi n} \] ..."
  • Page 261; line 7: H(e^(j\omega)) = j\omega j\omega / T_s

Chapter 10:

  • Page 280; Unnumbered equation after (10.6), 2nd line: there is a spurious "/" sign before the "2" in the denominator of the first term.
  • Page 290; Exercise 10.3: To solve this exercise the student needs the material in Chapter 11 first.

Chapter 11:

  • Page 297; Section 11.1.3, first equation: it should be X_{2D}(z)=\frac{1}{2}[X(z^{1/2})+X(-z^{1/2})].
  • Page 315; Equation (11.20): it should be X_c(j\Omega) = \frac{\pi}{\Omega_N} I(j\pi\Omega/\Omega_N) X(e^{j\pi\Omega/\Omega_N}).

Chapter 12:

  • Page 341; Formula for PAM power is missing a leading factor of two; final result is $\frac{2^M(2^M+3)+2}{12}$
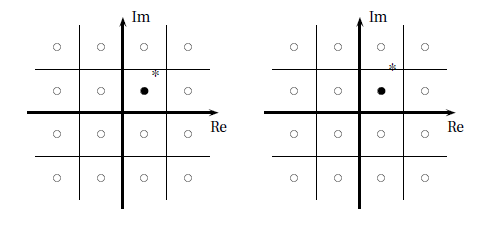
  • Page 345; Figure 12.14 got mangled in the typesetting. It should be like this:
  • Page 350; Figure 12.19 signal at the ouput of the diagram should be $\hat{c}[n]$
  • Page 358; Eq. 12.35 $x_{ND}[n] = \sin((2\pi \beta) n)$ $x_{ND}[n] = \sin(((2\pi/ \beta) n)$
  • Page 360; Eq 12:39 \hat{x}_\tau(n_0; \tau) \hat{x}(n_0; \tau)
  • Page 361; Eq 12.41: x_\beta[n] = x(nT_s - n\frac{1-\beta}{\beta}T_s) = x(nT_s - n\tau T_s) x_\beta[n] = x(nT_s + n\frac{1-\beta}{\beta}T_s) = x(nT_s + n\tau T_s)
  • Page 361; items 3 and 4: The prime ( ' ) should goon \tau and not on x . For instance in the very last line: $x_{\beta}[4] = x_{\tau'}[b]$
  • Page 362; items 3 and 4: The prime ( ' ) should goon \tau and not on x .